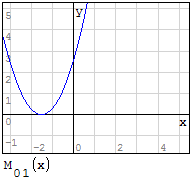
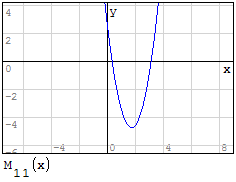
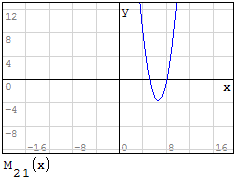
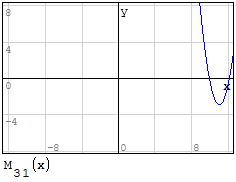
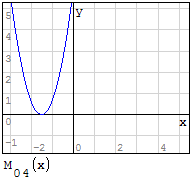
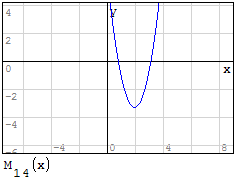
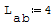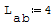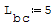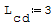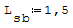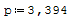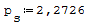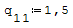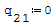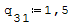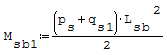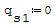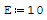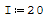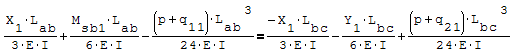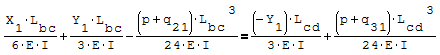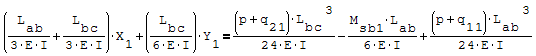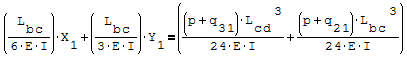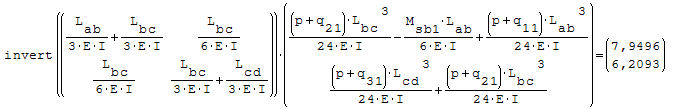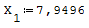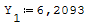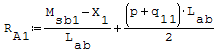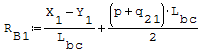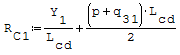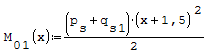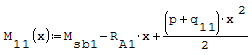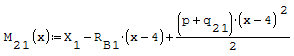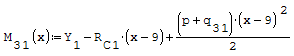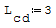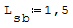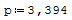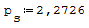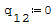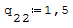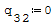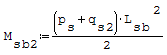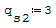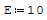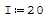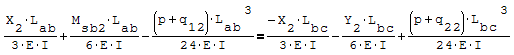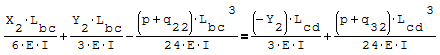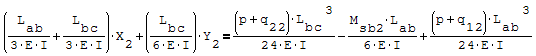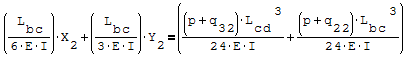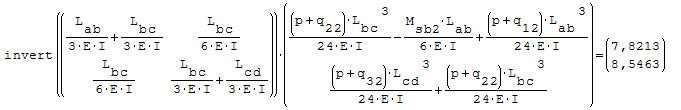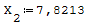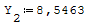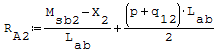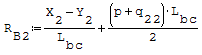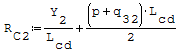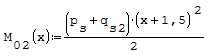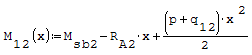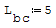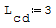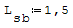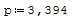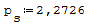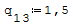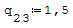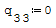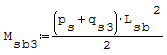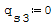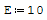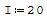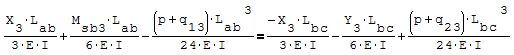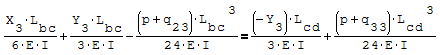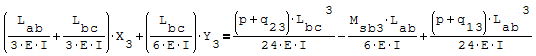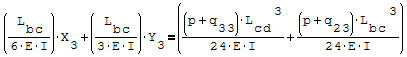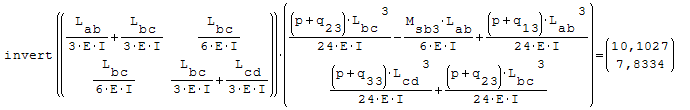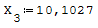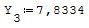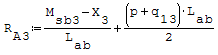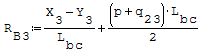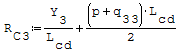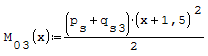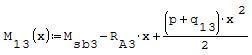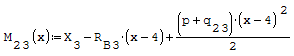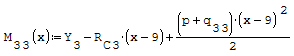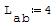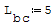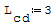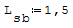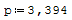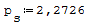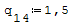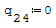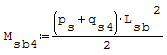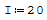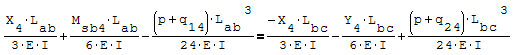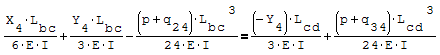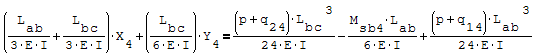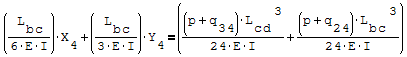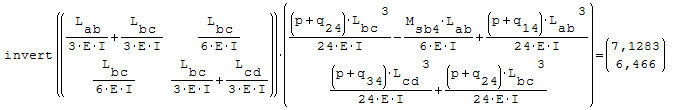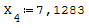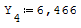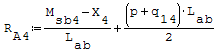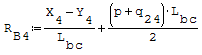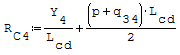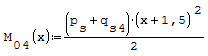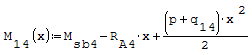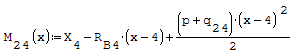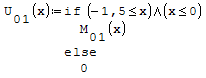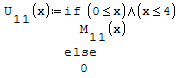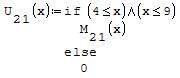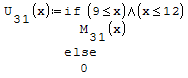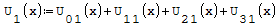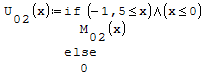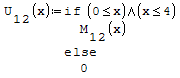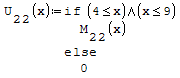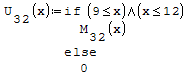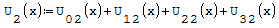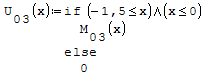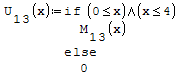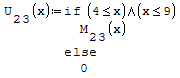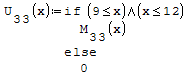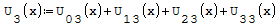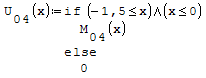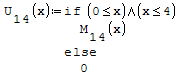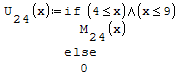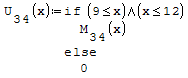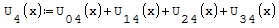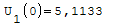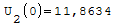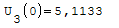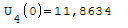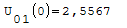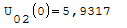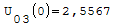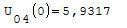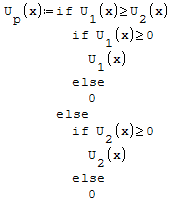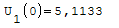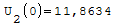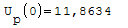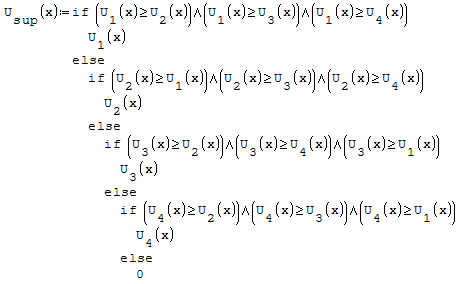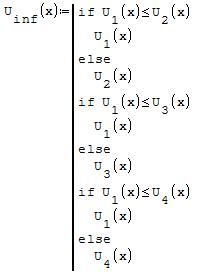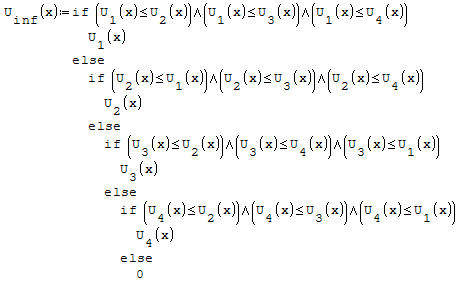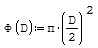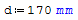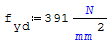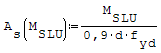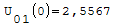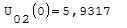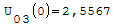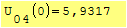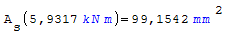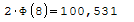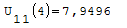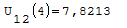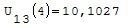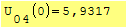1° SCHEMA

Cose che rimangono costanti:

Cose che variano a seconda dello schema:

Il modulo elastico e l'inerzia sono due numeri a casao nel calcolo sono indifferenti
perchè andrebbero a semplificarsi

Questa è il sistema di due equazioni in due incognite che deve essere risolto

Per risolverlo ho riportato le due equazioni nella forma canonica ax+by=c

Utilizzando l'algebra lineare la risoluzione equivale a Ax=B inv[A]*B=da la soluzione
del sistema

Reazioni vincolari generalizzate trovate a mano

Equazioni traslate a mano del momento

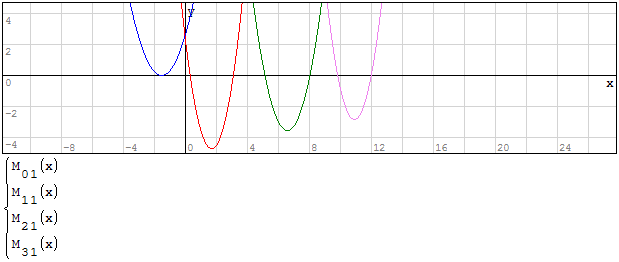
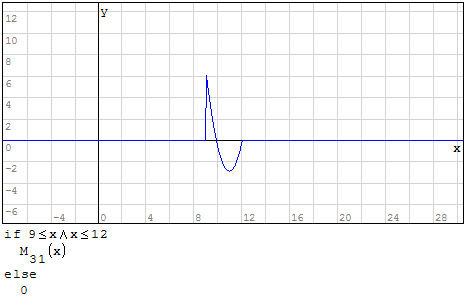
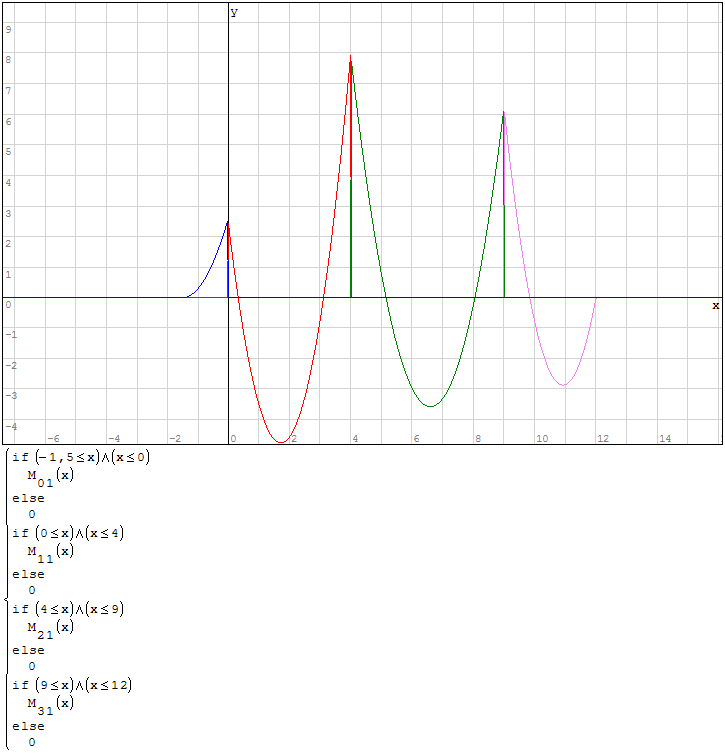
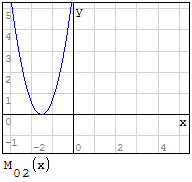
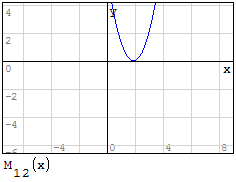
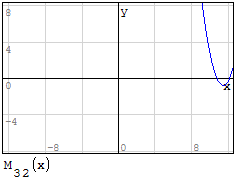
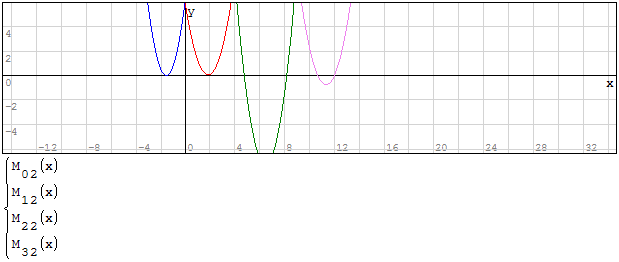
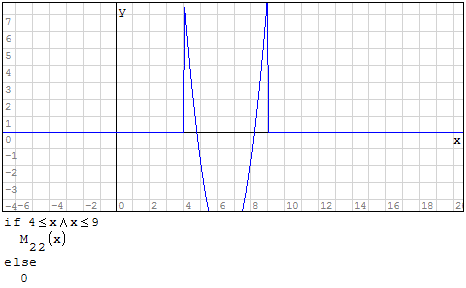
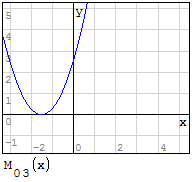
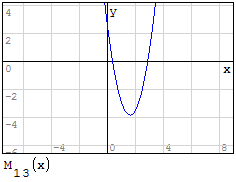
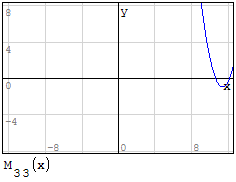
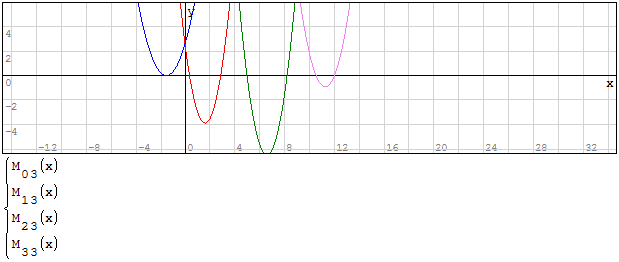
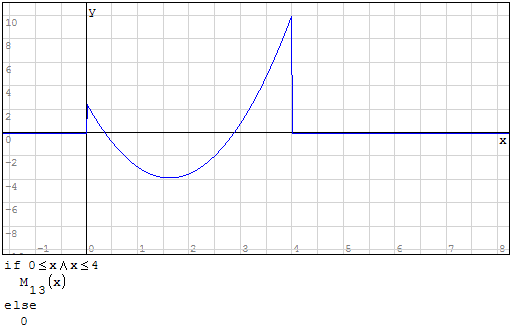
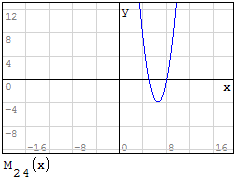
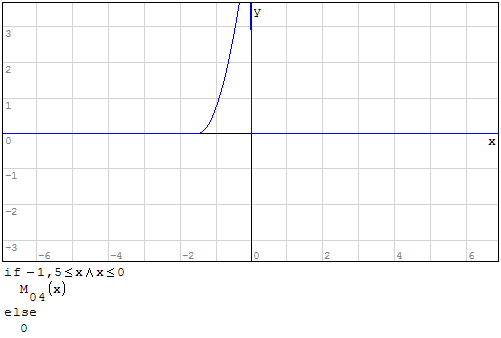
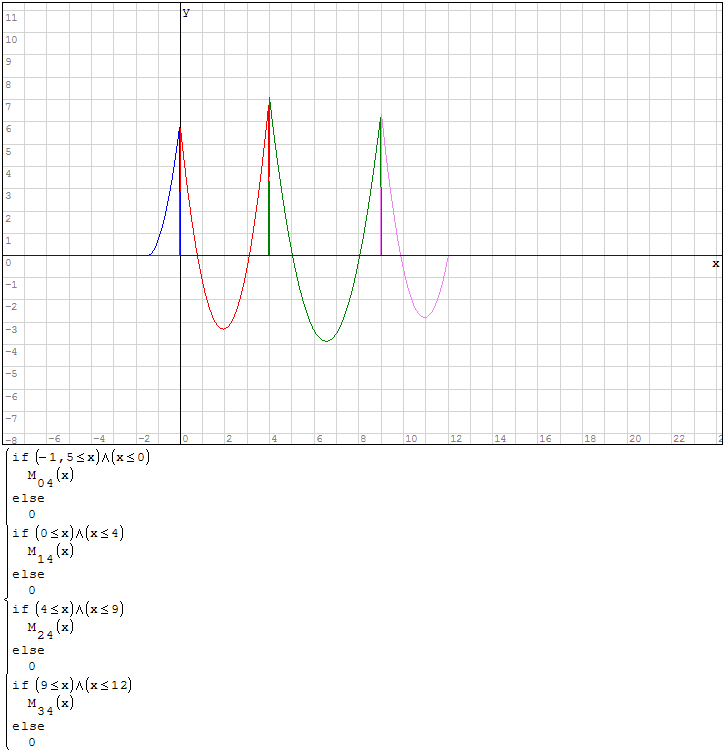
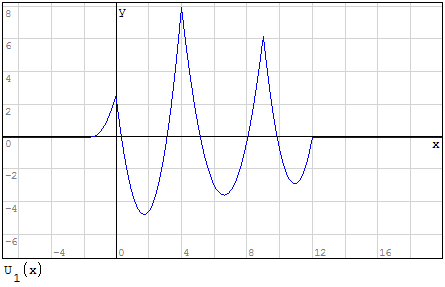
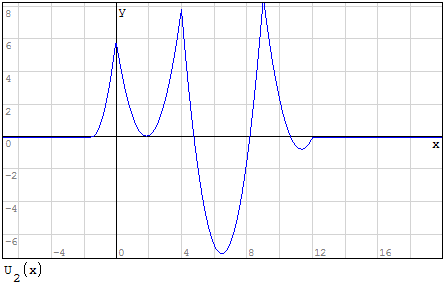
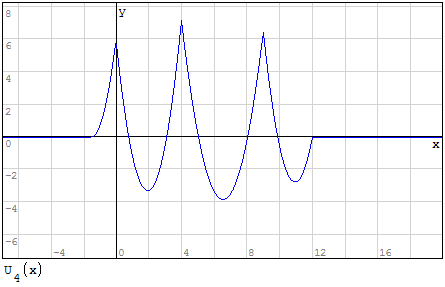
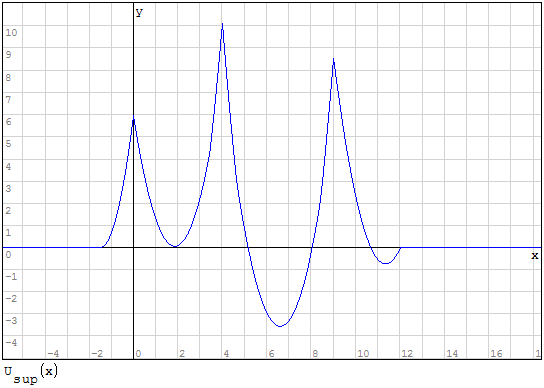
Funzioni in un unico grafico

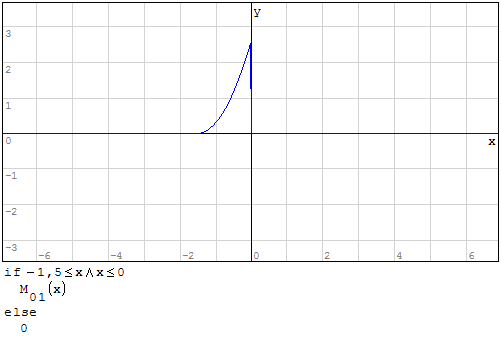
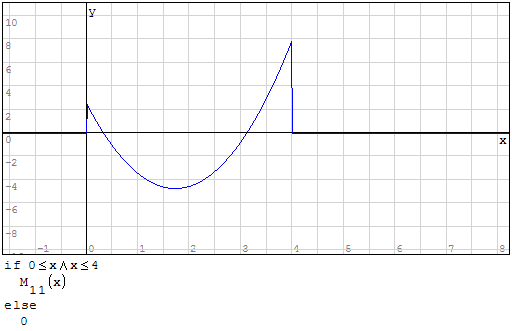
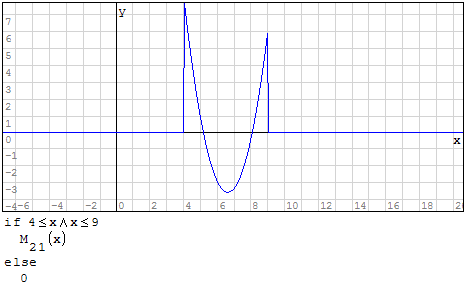
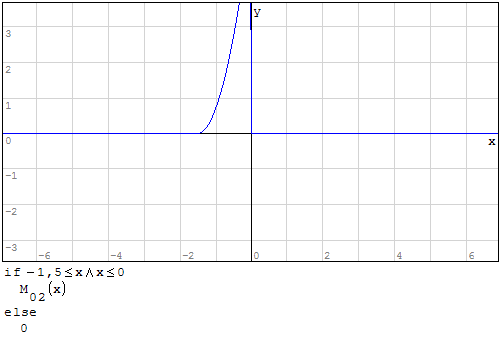
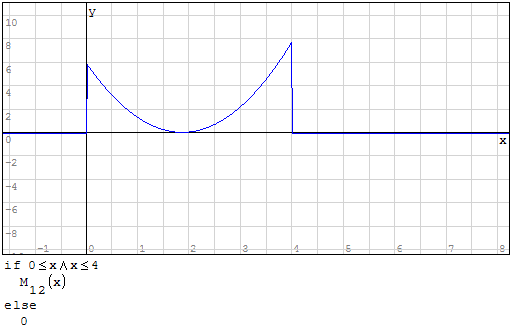
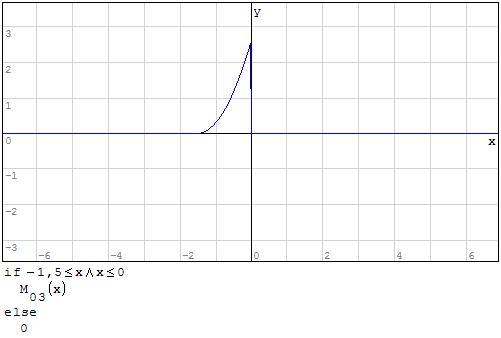
Per fare in modo che prenda solo il pezzo di parabola che mi interessa utilizzo la
funzione if

2° SCHEMA

Cose che rimangono costanti:

Cose che variano a seconda dello schema:

Il modulo elastico e l'inerzia sono due numeri a casao nel calcolo sono indifferenti
perchè andrebbero a semplificarsi

Questa è il sistema di due equazioni in due incognite che deve essere risolto

Per risolverlo ho riportato le due equazioni nella forma canonica ax+by=c

Utilizzando l'algebra lineare la risoluzione equivale a Ax=B inv[A]*B=da la soluzione
del sistema

Reazioni vincolari generalizzate trovate a mano

Equazioni traslate a mano del momento

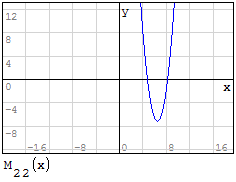
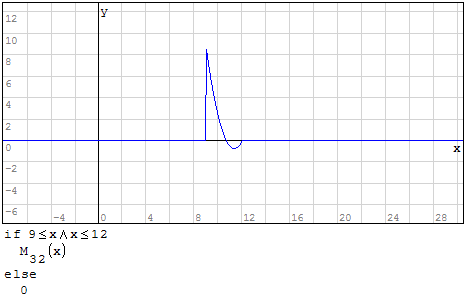
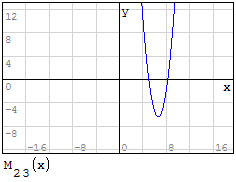
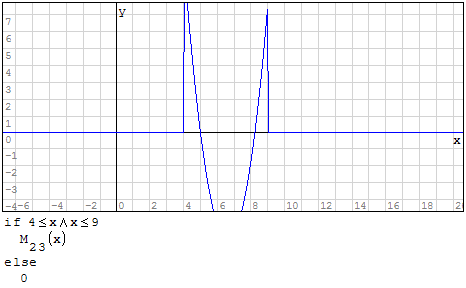
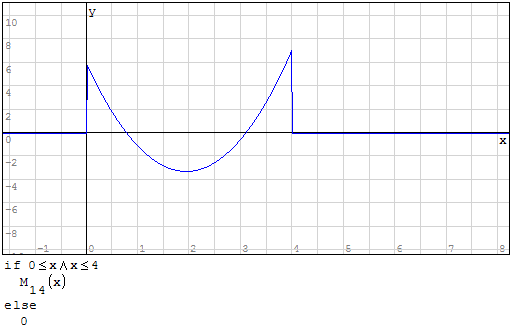
Funzioni in un unico grafico

Per fare in modo che prenda solo il pezzo di parabola che mi interessa utilizzo la
funzione if

3° SCHEMA

Cose che rimangono costanti:

Cose che variano a seconda dello schema:

Il modulo elastico e l'inerzia sono due numeri a casao nel calcolo sono indifferenti
perchè andrebbero a semplificarsi

Questa è il sistema di due equazioni in due incognite che deve essere risolto

Per risolverlo ho riportato le due equazioni nella forma canonica ax+by=c

Utilizzando l'algebra lineare la risoluzione equivale a Ax=B inv[A]*B=da la soluzione
del sistema

Reazioni vincolari generalizzate trovate a mano

Equazioni traslate a mano del momento

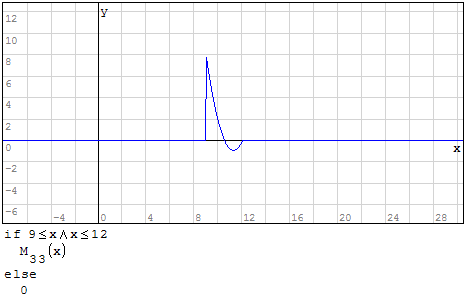
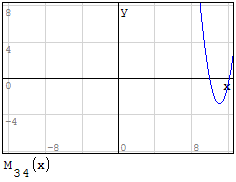
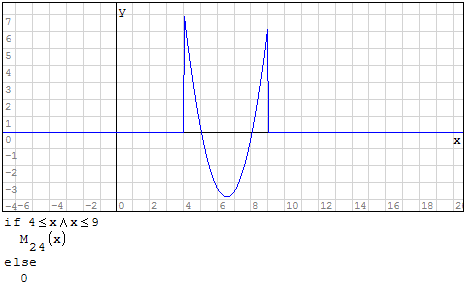
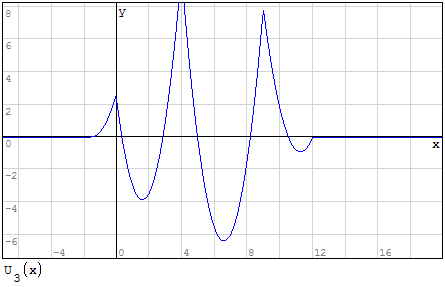
Funzioni in un unico grafico

Per fare in modo che prenda solo il pezzo di parabola che mi interessa utilizzo la
funzione if

4° SCHEMA

Cose che rimangono costanti:

Cose che variano a seconda dello schema:

Il modulo elastico e l'inerzia sono due numeri a casao nel calcolo sono indifferenti
perchè andrebbero a semplificarsi

Questa è il sistema di due equazioni in due incognite che deve essere risolto

Per risolverlo ho riportato le due equazioni nella forma canonica ax+by=c

Utilizzando l'algebra lineare la risoluzione equivale a Ax=B inv[A]*B=da la soluzione
del sistema

Reazioni vincolari generalizzate trovate a mano

Equazioni traslate a mano del momento

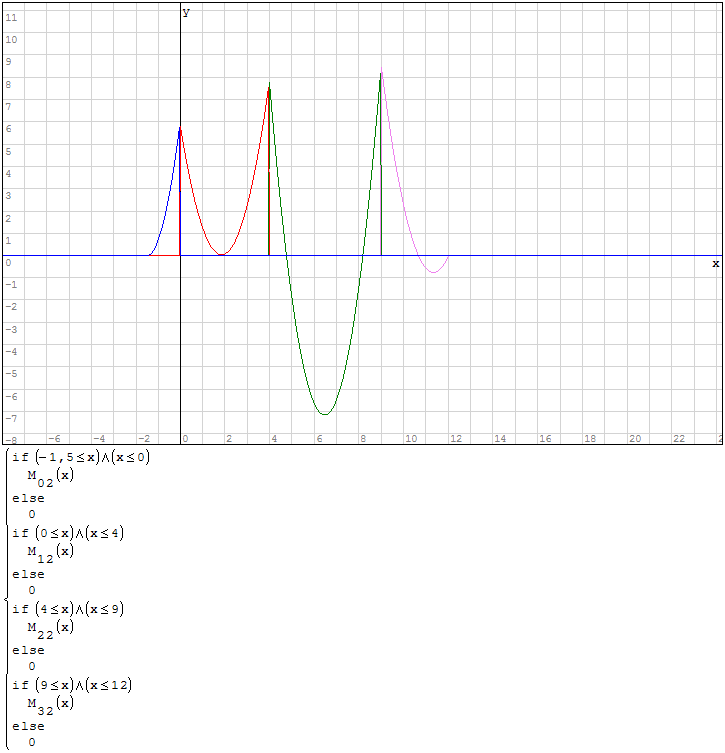
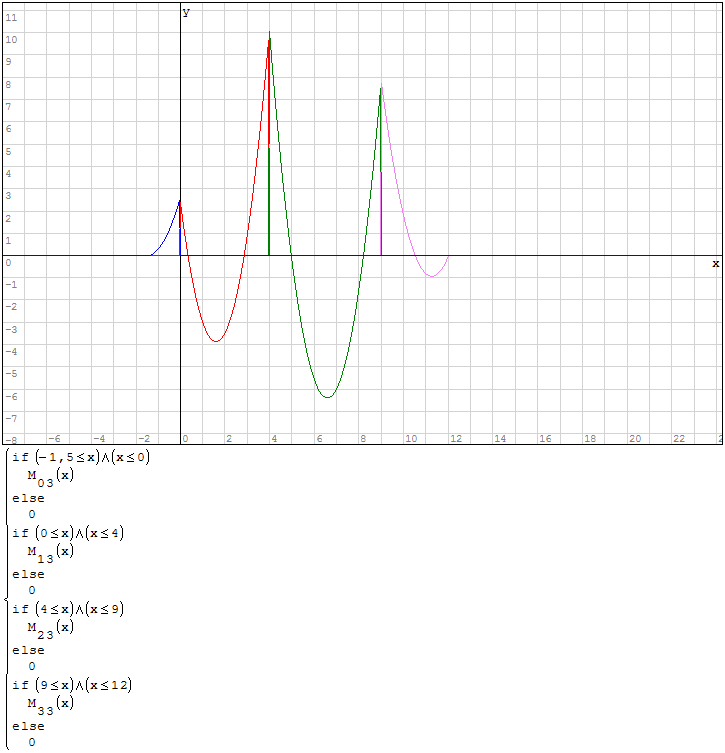
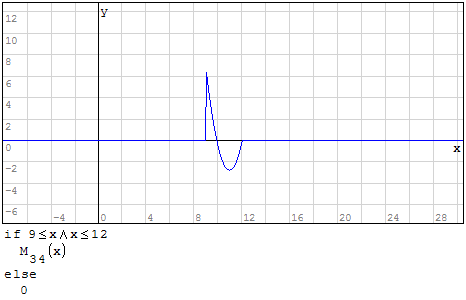
Funzioni in un unico grafico

Per fare in modo che prenda solo il pezzo di parabola che mi interessa utilizzo la
funzione if

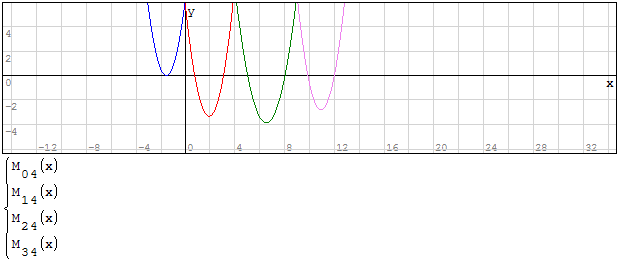
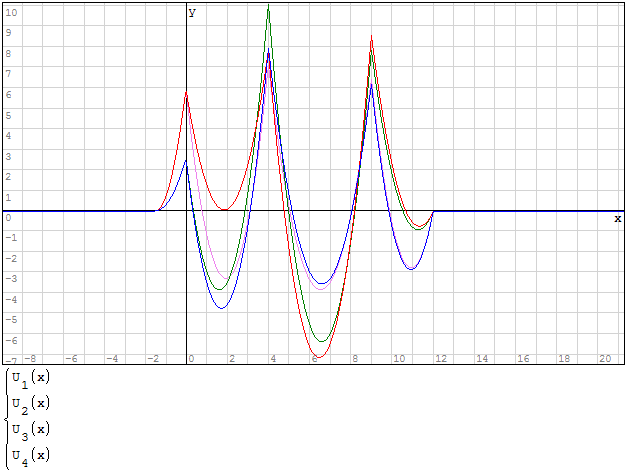
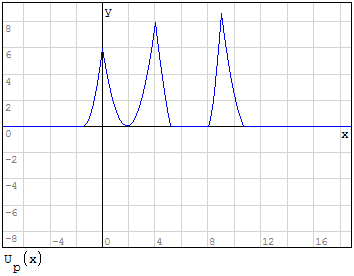
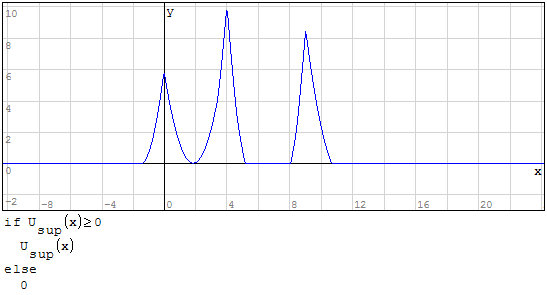
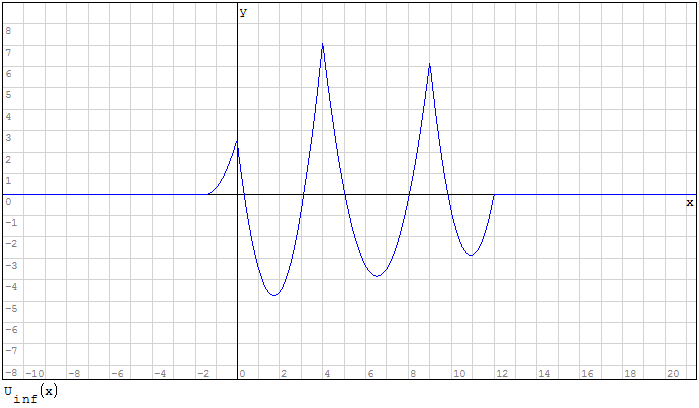
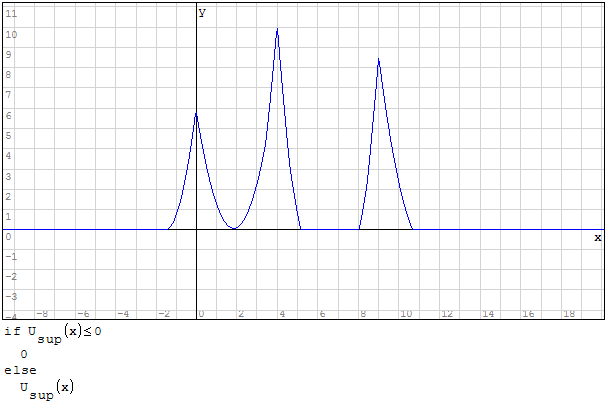
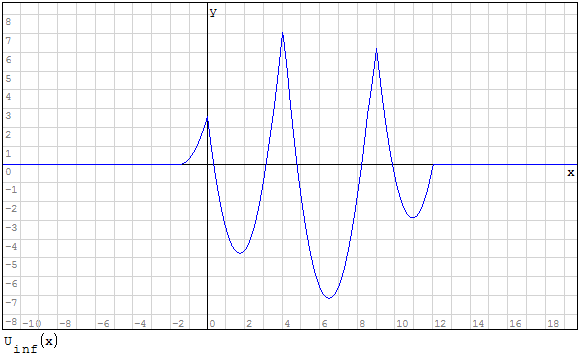
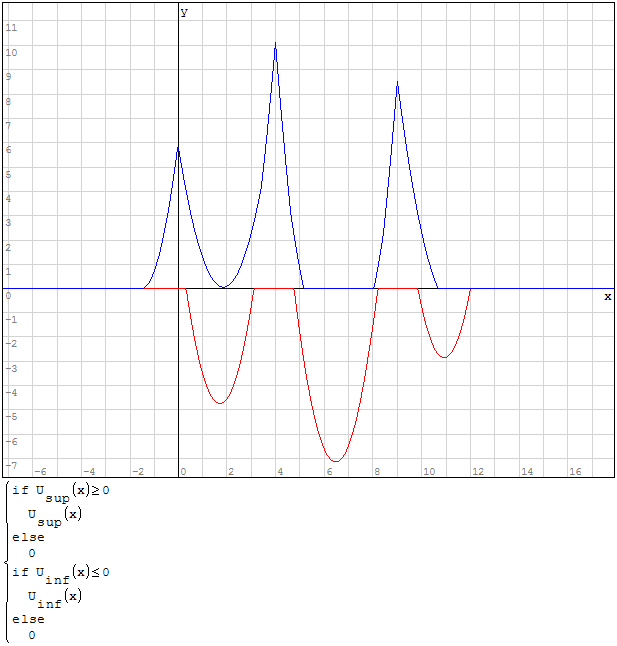
Devo creare l'inviluppo delle funzioni, questo significa prendere i valori maggiori per
l'inviluppo superiore ed i valori minori per l'inviluppo inferiore questo perchè devo
prendere i valori di momento maggiore.

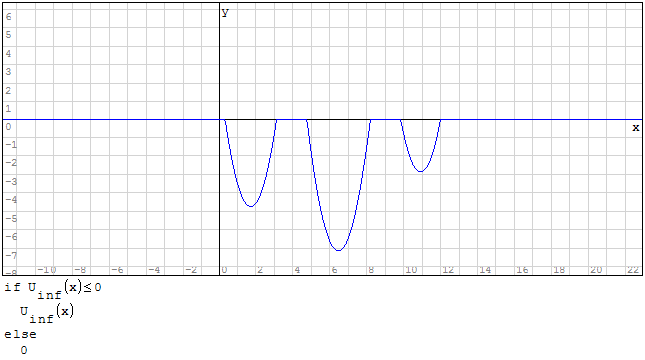
Per fare ciò posso utilizzare la funzione if, dicendo che se la funzione ha un valore
maggiore prendi qualla funzione altrimenti prendi quell'altra funzione. Per fare in
modo che i valori siano positivi imporre la condizione che il valore della funzione
deve essere maggiore di zero.

Calcolo dell'armatura:

Formula:

Nell'unione delle funzioni per creare i grafici succede un impiccio e i dati non sono
più corretti, devo utilizzare i dati prima e confrontarli a mano per avere il risultato
giusto

Nel punto zero qual'è il valore più alto?

Armatura superiori in ordine di picco:

Quantità di armatura necessaria nel punto zero

Due ferri della dimensione 8 bastano per far si che la struttura regga